COEFICIENTES BINOMIALES Y TEOREMA DE BINOMIOS
COEFICIENTE BINOMINALES
Los coeficientes binomiales, números combinatorios o combinaciones son números estudiados en combinatoria que corresponden al número de formas en que se pueden extraer subconjuntos a partir de un conjunto dado. Sin embargo, dependiendo del enfoque que tenga la exposición, se pueden usar otras definiciones equivalentes.
TEOREMA DE BINOMIOS
En matemática, el teorema del binomio es una fórmula que proporciona el desarrollo de la potencia n-ésima de n (siendo n, entero positivo) de un binomio. De acuerdo con el teorema, es posible expandir la potencia (x + y)n en una suma que implica términos de la forma axbyc, donde los exponentes b y c son números naturales con b + c = n, y el coeficiente a de cada término es un número entero positivo que depende de n y b. Cuando un exponente es cero, la correspondiente potencia es usualmente omitida del término. Por ejemplo,
El coeficiente a en los términos de xbyc - xcyb es conocido como el coeficiente binomial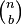 
o 
(los dos tienen el mismo valor).
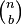o (los dos tienen el mismo valor).
No hay comentarios.:
Publicar un comentario